Inequalities

Inequalities are mathematical sentences that compare quantities (amounts or values) that are not equal.  Remember that the an equation is a mathematical sentence that relates two equal quanties.  For example 4+5 = 19-10.  An inequality might be written 4+5 < 19+10.

Notice the difference:  both sides of the equation have a value of 9, while the inquality has a value of 9 on the left and a value of 19 on the right.  Since the value of 19 is greater the symbol for greater stands in for the equal sign.

Symbols to Remember

< means "is less than"
> means "is greater than"
< means "is less than or equal to"
> means "is greater than or equal to"

Note: the word "is" is important to remember when describing an inequality because later you will be writing algebraic expressions from word phrases.  "Is less than" and "less than" mean two different things, where the phrase "less than" means to subtract and "is less than" signifies and inequality.

Graphing Inequalities on a Number Line

When graphing on a number line, any < or > inequality is graphed with an open circle. So x > 2 1/2 is graphed....

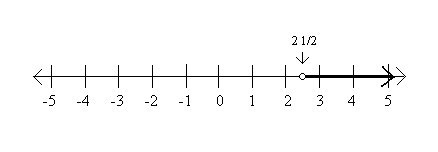
When graphing < or > , the graph uses a closed circle because value may be equal to the point on the number line.  So x < 2 1/2 is graphed...

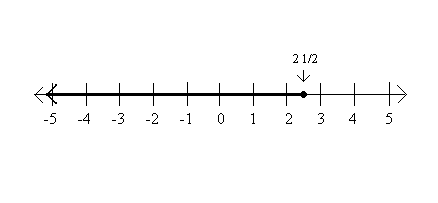
Graphs taken from: http://www.sparknotes.com/math/algebra1/inequalities/section4.rhtml

For more explanation take a look at this site.  

It gives a clear description of inequalities and graphing.

Inequalities (more notes)

Here is something that Mrs. Salinger created that you might find hopeful.


Inequality Notes

The Coordinate Plane

Above you will see an example of the coordinate plane.  The coordinate plane is a two dimensional surface on which you can plot points to create lines and curves.  

The plane is constructed by two axes - the x-axis and the y-axis.

The x-axis is the horizontal (left/right) scale or number line with negative numbers two the left of zero and decreasing in value and positive numbers to the right of zero increasing in value.

The y-axis is the vertical (up/down) scale or number line with negative numbers two the below zero and decreasing in value and positive numbers to the above zero increasing in value.

Where the x and y axes cross is called the origin and is noted as (0,0).

The x and y axes also create four separate sections on the plane and are called quadrants.  Quadrant I has both positive coordinates.  The rest of the quadrants are numbered in counter clockwise order. (See image above)

You plot points using a value of x (horizontal) and a value for y (vertical).  You need both values to plot a point and they are written as (x,y).  They can be called coordinates or ordered pairs.

Features to Think About

• You can tell whether a point lies on the x or y axis by looking at the coordinates
• If the y coordinate is zero then the point lies on the x axis
• If the x coordinate is zero then the point lies on the y axis
• This should make sense because if there is no value for y, for example, the point will be neither above or below the x-axis.
• Because of what was mentioned in the previous bullet, not all points will be placed in one of the four quadrants.  Some points will lie on either the x or y axis or on the origin iteself

Help Hints (Reasons for the Names)

• If you break the word COORDINATE into the prefix CO and the root ORDINATE, know that the prefix CO means 'together' and the root ordinate means 'place in orderly rows or regular fashion.'
• Think of ORIGIN is the beginning or a starting point
• Look at the word QUADRANT, 'quad' signifies 'four'
• To remember the order of your coordinates, think about why they are called ORDERED PAIRS.  Notice that they are written in alphabetical order (x,y).

Uses for the Coordinate Plane

• Navigation
• Business and Statistics to track and understand trends
• Scientists and Economists to analyze relationships

Image From:  http://www.learningwave.com/lwonline/algebra_section2/alg_coord.html

Plotting Practice

Click on the link below for a list of interactive resources you can use to practice plotting points on a coordinate plane.

http://www.internet4classrooms.com/skill_builders/coordinate_plane_math_sixth_6th_grade.htm

I personally like this Stock the Shelves game to increase your speed and accuracy.

Pep Talk

Integers and the Coordinate Plane Pretest

Integers and the Coordinate Plane Pre-Test

Absolute Value

Absolute value simply means the amount of "jumps" made on a number line.  It is a measurement of distance moved from one place on a number line to another.  Because it is measuring distance and not direction, absolute value is always positive.  The absolute value of a number is noted between two absolute value bars.

|-5| = 5

|7| = 7

If we take the absolute value of |-6|or|6| or and look at it as the distance from zero on the number line, you can see that in either direction you have moved six spaces.  You either move or you don't.  This is way the value is always positive.

Important to Remember: Absolute value bars are also considered grouping symbols.  Like parentheses, whatever operations occur inside the absolute value bars are done first in order of operations.

|5-2*6|=|5-12|=|-7|=7

Number Line Image taken from www.mathisfun.com

Integers & Rational Numbers

Welcome to the new unit on Integers and the Coordinate Plane.  In class we talked about two categories of numbers.  Integers are any positive or negative whole number including zero.  Essentially any whole number and its opposite is considered an integers (for example 4 and -4 are opposites).  The other category is called rational numbers.  Rational numbers are numbers that can be converted into fractions.  Decimals that repeat in consistent patterns or that terminate can be converted into fractions.  Numbers like pi or phi can not be converted into fractions because the decimal does not terminate and there is no consistent pattern with the digits.  These numbers are called irrational.

One clue to remember what a rational number is to look at the word rational itself.  RATIOnal.  Notice the root of the word is ratio.  Remember ratios are the comparison of one quantity to another (numerators as compared to denominators) and are typically written in fraction form.

A set of integers ordered least to greatest may be {-5, -1, 0, 4,  10}

A set of rational numbers ordered least to greatest may be {-3/5, -.25, 1, 1/2, .4444....} 

Fractions, Decimals, and Percent Conversions

Click on the link to go to the Math is Fun website to review your understanding of fraction, decimal, and percent conversion.  There is a great interactive manipulative for you to use.  My only issue with this page is when it explains how to convert decimals into percents and back into decimals again, it does not explain why you move the decimal two places.

Remember: converting a decimal to a percent requires you to multiply by 100 (percent means for every hundred).  You are moving the decimal to the right because you are multiplying by a number greater than one.  You are moving it twice because 100 is equivalent to 10 to the 2nd power which is equivalent to two place values.  Moving from a percent to a decimal requires you to divide by 100.  It should make sense that you would move the decimal to the left now because you number should get smaller.

Suggested Strategies for Comparing & Ordering Fractions

The following document was created by Mrs. A. Salinger. Comparing Fractions

Converting Decimals to Fractions

To convert decimals to fractions first you should remember that all decimal places have a base-ten place value.  So, the first place behind the decimal point is the tenths, the second place is the hundredths, the third place is the thousandths, and so on.

If you are given a decimal such as 0.312, simply say the decimal in the proper notation. ("three hundred twelve thousandths").  You should be able to 'hear' the denominator of your fraction.  Therefore the fraction form is 312/1000.

BUT WAIT!

You must always reduce your fractions to their simplest form.  Since the GCF of 312 and 1000 is 8,  take 312/1000 divide your numerator and denominator by 8/8 to get 39/125.  This is the fraction form of the decimal 0.312.

Comparing Fractions

Here is a quick overview of comparing fractions from Math is Fun.  You can cross multiply to see which fraction is greater.  However, remember that cross-multiplying is actually finding the common denominator by multiplying the two denominators together.  You are just skipping the step of writing the common denominator to compare.

For example:

Compare 2/3 to 5/7.  When you cross multiply 3*5 and 2*7 you'll see that 2/3 is less than 5/7.  What you're really doing is this 2/3 * 7/7 = 14/21 and 5/7* 3/3 = 15/21.  You should notice that the numerators are the same as the number you got when you cross multiplied.

Tradition Long Division Algorithm

Hi again,

The long division algorithm may take some getting used to, however, if you think about place values and stay organized, you'll see that it may take less brain power than using partial quotients.  If fact, the traditional algorithm allows you to divide more accurately in that you do not need to use remainders anymore.  By adding a decimal point and zeros to your dividend you can continue to divide with out changing the value of your dividend.  The video below show you the basic method when the divisot goes into the dividend evenly.

The image below is a clear example of another problem where the divisor goes into the divided evenly.  The letters down the side just show the steps.

You may have noticed the "crib" to the left of the image.  Some people will multiply the divisor by numbers 1-9 first to make the division work go more smoothly.  Ten is actually unnecessary because each place value can only be named by one digit.

The video below shows you a division problem where the remainder is converted into a decimal.

Traditional Multiplication Algorithm

Hi Everyone,  I know some of you have experience with the traditional multiplication algorithm and some of you prefer to use the lattice method.  There are many avenues to solve problems, some are better than others under certain circumstances.  With some practice, the traditional algorithm for multiplication will help you solve problems quickly and efficiently.

The video below explains the algorithm using the distributive property. 

When multiplying by more than one digit, you just have to remember what you know about place value. When multiplying and number by a multiple of 10, your product will always end in a zero.  Then same is true for multiplying by any multiple of 100, your product will always end in two zeros.  Keep this in mind when using the traditional algorithm because when you multiply by a new place value you will add the appropriate number of zeros to your product in the problem.  Here's an example, notice the bolded zero.  That is placed there because your are multiplying in the tens place.  If you had a third digit, you would add two zeros because your are multiplying by the hundreds place.

Here's another Khan Academy video for further explanation.

Converting Fractions to Decimals

In class we talked about three different strategies you can use to convert fractions into decimals.  It is my recommendation that you start with the easier strategies and work your way down.  When looking at a fraction to convert to a decimal first think about those benchmark fractions we talked about in class.  Hopefully you have memorized some and have noticed the patterns they create.  This will help you convert the fraction quickly.

Fraction Benchmark	Decimal Benchmark	Pattern
1/2	.5
1/4, 2/4, 3/4	.25, .5, .75	+0.25
1/8, 2/8, 3/8, 4/8, 5/8, 6/8,7/8	0.125, 0.25, 0.375, 0.5, 0.625...	+0.125
1/16, 3/16, 5/16….	0.0625, 0.125, 0.1875...	+0.0625
1/3, 2/3	.333..., 0.6666...	+0.3 (repeated)
1/6, 2/6, 3/6, 4/6, 5/6	0.166.., 0.33..., 0.5, 0.66..., 0.833..	+0.166...
1/9, 2/9, 3/9, 4/9, 5/9….	0.111..., 0.222...0.3333, 0.444	+0.1 (repeated)
1/5, 2/5, 3/5, 4/5	0.2, 0.4, 0.6, 0.8	+0.2
1/10, 2/10, 3/10, 4/10, 5/10, 6/10...	0.1, 0.2, 0.3	+0.1

If you can not remember the benchmarks or one does not exist, look to see if you can find a common denominator with a base ten number.  This works because our decimal system place values uses base ten numbers like, tenths, hundredths, thousandths and so on.  

Fractions	Decimals	Strategy
¼, ¾, ⅕ , ⅓, 7/10	See Above	Benchmark
12/16, 15/45, 21/30	0.75, 0.333..., 0.7	Reduce the fraction first then use Benchmark
14/25, 23/50, 19/20	0.56, 046, 0.95	All of the denominators are factors of 100.  Use equivalent fractions to determine decimal
4/125, 7/250	0.032, 0.028	Both denominators are factors of 1000

If all else fails the final strategy is a way to convert any fraction to a decimal.  You need to use the traditional division algorithm.  Sometimes these problems do not work out nicely and the decimal continues on.  I have asked you to round to the nearest hundredth in this case.  This means you need to divide up to the thousandths place to be able to round the hundredths.

Converting Fractions Using Long Division

Some fractions are more difficult to convert into decimals because either they do not have an easy benchmark to remember or do not into a base ten denominator easily.  Therefore, the only way to convert is to divide the denominator into the numerator to get the decimal value of the fraction.  This method will work for any fraction.

Steps

1.  Your denominator is your divisor (the number that is doing the dividing) and your numerator is the dividend (the number that is being broken apart.  Set up your problem like this.  The image is a bit misleading. Notice that a decimal point and zeros should be added to the dividend since it is smaller than the divisor.  This allows you to compute.

2. Divide.  The following fraction works out evenly.  Many times this does not happen.  If that is the case be sure to read the directions on your assignment. Usually the directions will ask you to round to the nearest hundredth.  If there are no directions, it is safe to assume to round to the nearest hundredth.  This means you need to divide up to the thousandths place to determine whether you round up or not.

Bits & Pieces I Pretest

Bits & Pieces I Pretest

More Fun (Thanks Mrs. Schwartz)

Just for Fun!

Why Prime Factorization Matters

The following video gives you a preview of some of the work we will be doing in the next unit. I briefly demonstrated how you could use prime factorization to reduce fractions to a couple of the classes. I will go into more detail about this in the future. But for now, this video is a great explanation and demonstrates the power of prime factorization.

Explanation of prime factorization

The following video is a good review of prime factorization.  Prime factorizations is possible because of the Fundamental Theorem of Arithmetic.  Think about what the word fundamental means.  It means the basis of something.  Therefore the Fundamental Theorem describes the basis of numbers which are products of their prime factors and therefore unique!

A little inspiration..

More GCF & LCM Word Problem Guidance (Cobb County School District

Finding LCM Using Prime Factorization

Like GCF, you can use prime factorization to find the LCM of two or more numbers.  First find the GCF since the LCM and both numbers will share this factor.

Then multiply the GCF to all the remaining prime factors.  You are doing this because the prime factor string for the LCM must account for all the prime factors in your original numbers.  If not then you do not have the LCM.

Notice every prime in the prime factor string for the LCM (2160) is used at least once.  It is important to understand that the prime factor string for the LCM (2160 in this case) is the shortest factor string possible that will account for the prime factor strings of 144 and 1080.  This is the very meaning of least common multiple.  If you multiply the factor sting for 2160 by 2, you have a common multiple of 144 and 1080 but it is not the least common multiple.

Finding GCF using Prime Factorization

You have lots of experience finding the greatest common factor with various methods (u-turn, listing, rainbow).  However, the most efficient way to find the GCF for any two or more numbers, especially large numbers, is to use prime factorization.  Remember, the prime factor string for any number is unique.  Breaking numbers down into their basic prime factors allows us to manipulate them in ways that help us do things like find GCF and LCM of numbers.  For those of us that stress over simplifying large fractions, prime factorization is invaluable.  See below.

Notice only the COMMON primes between the two numbers are highlight in red.  When you multiply these common primes together you get a product of 72.  This is the greatest factor that is shared among the two numbers.  You may also notice that 12 is a common factor because the prime factor string 2 x 2 x 2 x 3 is found within both of the factor strings of 144 and 1080.  Can you find more common factors of these two number just by looking at their prime factor strings?

Hopefully, you're thinking to yourself why would we need to know this.  Look at the image below.  You can use prime factorization to simply fractions with large numerators and denominators instead of painstakingly using divisibility rules and dividing!

For those of you who want to go deeper, you can find the GCF for any number of numbers.  You just need to make sure each number shares the common primes. Look!

If you need a refresher with prime factorization watch this video.

GCF & LCM Word Problems

Deciding whether to use common multiples or common factors to solve problems can be tricky.  Therefore to remember:     

GCF problems involve sharing/dividing evenly

 LCM problems involve things happening in  cycles/ same time

Here's a sample problem:  

There are 40 girls and 32 boys who want to participate on co-ed soccer intramural teams.  If each team must have the same number of girls and the same number of boys, what is that greatest number of teams that could participate?  How many boys will be on each team?  How many girls on each team?

Think about what you are being asked to do with the values you are given.  In this case you are being asked to divide/split your numbers into equal groups.  This is your hint to begin to find factors.  Best practice is to use the u-turn method to ensure that you find all the factors of a number in an organized manner.  When the problem asks for the "greatest" number it is asking for the greatest common factor (GCF).  Keep in mind greatest doesn't mean multiple even though multiples create larger and larger numbers.  Also be sure you are answering what is being asked.  Even though you may have found the GCF, you have to use it to answer the rest of the questions

Here's another sample:

Ms. Pearl is shopping at the supermarket.  She is getting things for the sandwiches she is going to prepare for next Sunday's picnic.  She sees that hamburger buns come in packs of 8 but the hamburgers themselves come in packs of 10.  What is the least number of packs of buns and burgers she should get so she has an equal number of buns and burgers?

For this problem you will need to find multiples because it only makes sense that you will be increasing the number of packs to be able to get equal numbers.  Because it is asking for the least number of packs you will be finding least common multiple (LCM).  However, the LCM only tells you the number of buns and hamburgers (which is 40 in this case) so you will have to use it to determine the number of packs of each type of item.

Prime Time Pretest

Prime Time Pretest

Things to think about for Thursday's Quiz...

Your first quiz of the year is this Thursday 9.18.13.  Here are some things to review:

• Finding factors of a number
• Finding Proper Factors of a number
• Describing the best moves on the factor game and why they are the best moves
• Describing a set of numbers in relation to their divisibility rules.  For example, list the multiples of 12 up to 100 and describe the divisibility rules for the multiples
• Describe what makes a number prime
• Describe the reasons why certain numbers do not appear on the Product Game board while others do
• Know and use various divisibility rules
• Identify primes and composites
• Name at least two...
• abundant numbers
• deficient numbers
• perfect numbers 
• square numbers

Additional Important Vocabulary

Learning Vocabulary

The vocabulary assigned to various math ideas and concepts is not arbitrary (random). Often the words that name ideas and concepts actually describe the idea or concept.   For example, the term abundant number is used to describe a number in which the sum of the proper factors is greater than the number itself.  The word abundant means many, a lot, or sometimes excess.  If we understand the reason for the vocabulary we can better makes sense of the concepts.

Additionally, there are many strategies to understand and make sense of vocabulary.  The strategy of words maps is used below.  Understanding the vocabulary in math or science is half the battle in understanding the content of each subject.

Bits & Pieces III Pre-Test

Bits and Pieces III _Pre-Test_

Volume of a Rectangular Prism

Volume of Rectangular Prisms

by: R. W.

A rectangular prism is a three dimensional figure so it has space inside called volume. Volume is the amount of room a three dimensional figure takes up. To find the rectangular prisms volume, you need to know the formula. The volume is length times width times height or v=lwh.

To find the volume of this prism, we have to use the formula.

v=lwh

v= (3*6)*2

v= 18*2

v= 36 cubed feet

Angles

Trapezoids

Post by: J.T.