Remember from class we discussed the difference between numerical expressions and algebraic expressions. Algebraic expressions contain a variable. Also remember that expressions are part of equations. An equation is demonstrating two expressions that are equal. For example the equation y + 6 = x + 5 has two algebraic expressions which you know are equivalent given the equal sign.
To evaluate algebraic expressions you must know the value of the variable. The values of the variables will always be given. Here's an example:
Evaluate the expression 4b + 3c - 10 for b=5 and c=2.
To evaluate simply substitute the value of the variable and follow order of operations. In class, I expect to see the substitution. This is the expectation:
4(5) + 3(2) - 10 This shows the substitution
20 + 6 - 10 This demonstrates following the orders of operations
26 - 10
16 Solution
Here's another
Evaluate x^y - xyz + 6(z - y) when x=2, y=3, and z=(-1)
2^3 - (2)(3)(-1) + 6(-1 - 3)
8 - (-6) + 6(-4)
8 + 6 + (-24)
14 + (-24)
(-10)
Mr. Lattanzi's Math Blog
Friday, January 10, 2014
Thursday, January 9, 2014
Writing Algebraic Expressions From Word Phrases
This can be challenging, however it is important to take your time and make sense of the problem. Unfortunately there are no hard and fast rules (like integers) to interpret the word phrases into algebraic expressions, so we need to practice. One of the harder phrases involve subtraction. Look at the list below and be sure to study these phrases.
- A number less 9.........................n - 9
- A number less than 9.................9 - n
- A number is less than 9..............n < 9
Tuesday, November 12, 2013
Inequalities
Inequalities are mathematical sentences that compare quantities (amounts or values) that are not equal. Remember that the an equation is a mathematical sentence that relates two equal quanties. For example 4+5 = 19-10. An inequality might be written 4+5 < 19+10.
Notice the difference: both sides of the equation have a value of 9, while the inquality has a value of 9 on the left and a value of 19 on the right. Since the value of 19 is greater the symbol for greater stands in for the equal sign.
Symbols to Remember
< means "is less than"
> means "is greater than"
< means "is less than or equal to"
> means "is greater than or equal to"
Note: the word "is" is important to remember when describing an inequality because later you will be writing algebraic expressions from word phrases. "Is less than" and "less than" mean two different things, where the phrase "less than" means to subtract and "is less than" signifies and inequality.
Graphing Inequalities on a Number Line
When graphing on a number line, any < or > inequality is graphed with an open circle. So x > 2 1/2 is graphed....
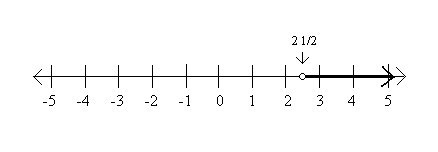
When graphing < or > , the graph uses a closed circle because value may be equal to the point on the number line. So x < 2 1/2 is graphed...
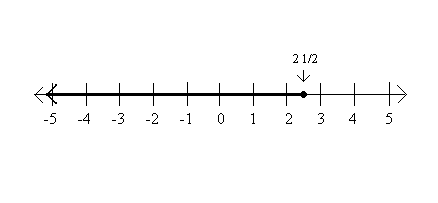
Notice the difference: both sides of the equation have a value of 9, while the inquality has a value of 9 on the left and a value of 19 on the right. Since the value of 19 is greater the symbol for greater stands in for the equal sign.
Symbols to Remember
< means "is less than"
> means "is greater than"
< means "is less than or equal to"
> means "is greater than or equal to"
Note: the word "is" is important to remember when describing an inequality because later you will be writing algebraic expressions from word phrases. "Is less than" and "less than" mean two different things, where the phrase "less than" means to subtract and "is less than" signifies and inequality.
Graphing Inequalities on a Number Line
When graphing on a number line, any < or > inequality is graphed with an open circle. So x > 2 1/2 is graphed....
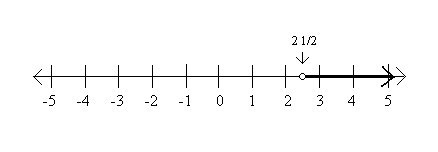
When graphing < or > , the graph uses a closed circle because value may be equal to the point on the number line. So x < 2 1/2 is graphed...

Graphs taken from: http://www.sparknotes.com/math/algebra1/inequalities/section4.rhtml
The Coordinate Plane
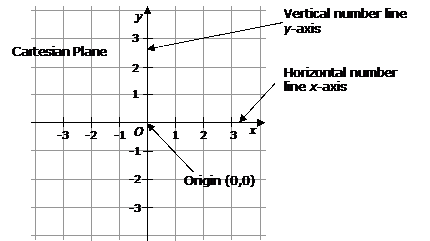
Above you will see an example of the coordinate plane. The coordinate plane is a two dimensional surface on which you can plot points to create lines and curves.
The plane is constructed by two axes - the x-axis and the y-axis.
The x-axis is the horizontal (left/right) scale or number line with negative numbers two the left of zero and decreasing in value and positive numbers to the right of zero increasing in value.
The y-axis is the vertical (up/down) scale or number line with negative numbers two the below zero and decreasing in value and positive numbers to the above zero increasing in value.
Where the x and y axes cross is called the origin and is noted as (0,0).
The x and y axes also create four separate sections on the plane and are called quadrants. Quadrant I has both positive coordinates. The rest of the quadrants are numbered in counter clockwise order. (See image above)
You plot points using a value of x (horizontal) and a value for y (vertical). You need both values to plot a point and they are written as (x,y). They can be called coordinates or ordered pairs.
Features to Think About
- You can tell whether a point lies on the x or y axis by looking at the coordinates
- If the y coordinate is zero then the point lies on the x axis
- If the x coordinate is zero then the point lies on the y axis
- This should make sense because if there is no value for y, for example, the point will be neither above or below the x-axis.
- Because of what was mentioned in the previous bullet, not all points will be placed in one of the four quadrants. Some points will lie on either the x or y axis or on the origin iteself
Help Hints (Reasons for the Names)
- If you break the word COORDINATE into the prefix CO and the root ORDINATE, know that the prefix CO means 'together' and the root ordinate means 'place in orderly rows or regular fashion.'
- Think of ORIGIN is the beginning or a starting point
- Look at the word QUADRANT, 'quad' signifies 'four'
- To remember the order of your coordinates, think about why they are called ORDERED PAIRS. Notice that they are written in alphabetical order (x,y).
- Navigation
- Business and Statistics to track and understand trends
- Scientists and Economists to analyze relationships
Monday, November 11, 2013
Plotting Practice
Click on the link below for a list of interactive resources you can use to practice plotting points on a coordinate plane.
http://www.internet4classrooms.com/skill_builders/coordinate_plane_math_sixth_6th_grade.htm
I personally like this Stock the Shelves game to increase your speed and accuracy.
http://www.internet4classrooms.com/skill_builders/coordinate_plane_math_sixth_6th_grade.htm
I personally like this Stock the Shelves game to increase your speed and accuracy.
Subscribe to:
Posts (Atom)





