Pep Talk

Integers and the Coordinate Plane Pretest

Integers and the Coordinate Plane Pre-Test

Absolute Value

Absolute value simply means the amount of "jumps" made on a number line.  It is a measurement of distance moved from one place on a number line to another.  Because it is measuring distance and not direction, absolute value is always positive.  The absolute value of a number is noted between two absolute value bars.

|-5| = 5

|7| = 7

If we take the absolute value of |-6|or|6| or and look at it as the distance from zero on the number line, you can see that in either direction you have moved six spaces.  You either move or you don't.  This is way the value is always positive.

Important to Remember: Absolute value bars are also considered grouping symbols.  Like parentheses, whatever operations occur inside the absolute value bars are done first in order of operations.

|5-2*6|=|5-12|=|-7|=7

Number Line Image taken from www.mathisfun.com

Integers & Rational Numbers

Welcome to the new unit on Integers and the Coordinate Plane.  In class we talked about two categories of numbers.  Integers are any positive or negative whole number including zero.  Essentially any whole number and its opposite is considered an integers (for example 4 and -4 are opposites).  The other category is called rational numbers.  Rational numbers are numbers that can be converted into fractions.  Decimals that repeat in consistent patterns or that terminate can be converted into fractions.  Numbers like pi or phi can not be converted into fractions because the decimal does not terminate and there is no consistent pattern with the digits.  These numbers are called irrational.

One clue to remember what a rational number is to look at the word rational itself.  RATIOnal.  Notice the root of the word is ratio.  Remember ratios are the comparison of one quantity to another (numerators as compared to denominators) and are typically written in fraction form.

A set of integers ordered least to greatest may be {-5, -1, 0, 4,  10}

A set of rational numbers ordered least to greatest may be {-3/5, -.25, 1, 1/2, .4444....} 

Fractions, Decimals, and Percent Conversions

Click on the link to go to the Math is Fun website to review your understanding of fraction, decimal, and percent conversion.  There is a great interactive manipulative for you to use.  My only issue with this page is when it explains how to convert decimals into percents and back into decimals again, it does not explain why you move the decimal two places.

Remember: converting a decimal to a percent requires you to multiply by 100 (percent means for every hundred).  You are moving the decimal to the right because you are multiplying by a number greater than one.  You are moving it twice because 100 is equivalent to 10 to the 2nd power which is equivalent to two place values.  Moving from a percent to a decimal requires you to divide by 100.  It should make sense that you would move the decimal to the left now because you number should get smaller.

Suggested Strategies for Comparing & Ordering Fractions

The following document was created by Mrs. A. Salinger. Comparing Fractions

Converting Decimals to Fractions

To convert decimals to fractions first you should remember that all decimal places have a base-ten place value.  So, the first place behind the decimal point is the tenths, the second place is the hundredths, the third place is the thousandths, and so on.

If you are given a decimal such as 0.312, simply say the decimal in the proper notation. ("three hundred twelve thousandths").  You should be able to 'hear' the denominator of your fraction.  Therefore the fraction form is 312/1000.

BUT WAIT!

You must always reduce your fractions to their simplest form.  Since the GCF of 312 and 1000 is 8,  take 312/1000 divide your numerator and denominator by 8/8 to get 39/125.  This is the fraction form of the decimal 0.312.

Comparing Fractions

Here is a quick overview of comparing fractions from Math is Fun.  You can cross multiply to see which fraction is greater.  However, remember that cross-multiplying is actually finding the common denominator by multiplying the two denominators together.  You are just skipping the step of writing the common denominator to compare.

For example:

Compare 2/3 to 5/7.  When you cross multiply 3*5 and 2*7 you'll see that 2/3 is less than 5/7.  What you're really doing is this 2/3 * 7/7 = 14/21 and 5/7* 3/3 = 15/21.  You should notice that the numerators are the same as the number you got when you cross multiplied.

Tradition Long Division Algorithm

Hi again,

The long division algorithm may take some getting used to, however, if you think about place values and stay organized, you'll see that it may take less brain power than using partial quotients.  If fact, the traditional algorithm allows you to divide more accurately in that you do not need to use remainders anymore.  By adding a decimal point and zeros to your dividend you can continue to divide with out changing the value of your dividend.  The video below show you the basic method when the divisot goes into the dividend evenly.

The image below is a clear example of another problem where the divisor goes into the divided evenly.  The letters down the side just show the steps.

You may have noticed the "crib" to the left of the image.  Some people will multiply the divisor by numbers 1-9 first to make the division work go more smoothly.  Ten is actually unnecessary because each place value can only be named by one digit.

The video below shows you a division problem where the remainder is converted into a decimal.

Traditional Multiplication Algorithm

Hi Everyone,  I know some of you have experience with the traditional multiplication algorithm and some of you prefer to use the lattice method.  There are many avenues to solve problems, some are better than others under certain circumstances.  With some practice, the traditional algorithm for multiplication will help you solve problems quickly and efficiently.

The video below explains the algorithm using the distributive property. 

When multiplying by more than one digit, you just have to remember what you know about place value. When multiplying and number by a multiple of 10, your product will always end in a zero.  Then same is true for multiplying by any multiple of 100, your product will always end in two zeros.  Keep this in mind when using the traditional algorithm because when you multiply by a new place value you will add the appropriate number of zeros to your product in the problem.  Here's an example, notice the bolded zero.  That is placed there because your are multiplying in the tens place.  If you had a third digit, you would add two zeros because your are multiplying by the hundreds place.

Here's another Khan Academy video for further explanation.

Converting Fractions to Decimals

In class we talked about three different strategies you can use to convert fractions into decimals.  It is my recommendation that you start with the easier strategies and work your way down.  When looking at a fraction to convert to a decimal first think about those benchmark fractions we talked about in class.  Hopefully you have memorized some and have noticed the patterns they create.  This will help you convert the fraction quickly.

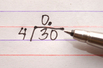
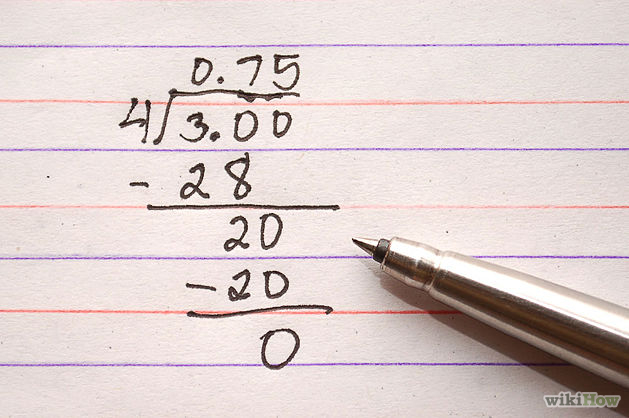
Fraction Benchmark	Decimal Benchmark	Pattern
1/2	.5
1/4, 2/4, 3/4	.25, .5, .75	+0.25
1/8, 2/8, 3/8, 4/8, 5/8, 6/8,7/8	0.125, 0.25, 0.375, 0.5, 0.625...	+0.125
1/16, 3/16, 5/16….	0.0625, 0.125, 0.1875...	+0.0625
1/3, 2/3	.333..., 0.6666...	+0.3 (repeated)
1/6, 2/6, 3/6, 4/6, 5/6	0.166.., 0.33..., 0.5, 0.66..., 0.833..	+0.166...
1/9, 2/9, 3/9, 4/9, 5/9….	0.111..., 0.222...0.3333, 0.444	+0.1 (repeated)
1/5, 2/5, 3/5, 4/5	0.2, 0.4, 0.6, 0.8	+0.2
1/10, 2/10, 3/10, 4/10, 5/10, 6/10...	0.1, 0.2, 0.3	+0.1

If you can not remember the benchmarks or one does not exist, look to see if you can find a common denominator with a base ten number.  This works because our decimal system place values uses base ten numbers like, tenths, hundredths, thousandths and so on.  

Fractions	Decimals	Strategy
¼, ¾, ⅕ , ⅓, 7/10	See Above	Benchmark
12/16, 15/45, 21/30	0.75, 0.333..., 0.7	Reduce the fraction first then use Benchmark
14/25, 23/50, 19/20	0.56, 046, 0.95	All of the denominators are factors of 100.  Use equivalent fractions to determine decimal
4/125, 7/250	0.032, 0.028	Both denominators are factors of 1000

If all else fails the final strategy is a way to convert any fraction to a decimal.  You need to use the traditional division algorithm.  Sometimes these problems do not work out nicely and the decimal continues on.  I have asked you to round to the nearest hundredth in this case.  This means you need to divide up to the thousandths place to be able to round the hundredths.

Converting Fractions Using Long Division

Some fractions are more difficult to convert into decimals because either they do not have an easy benchmark to remember or do not into a base ten denominator easily.  Therefore, the only way to convert is to divide the denominator into the numerator to get the decimal value of the fraction.  This method will work for any fraction.

Steps

1.  Your denominator is your divisor (the number that is doing the dividing) and your numerator is the dividend (the number that is being broken apart.  Set up your problem like this.  The image is a bit misleading. Notice that a decimal point and zeros should be added to the dividend since it is smaller than the divisor.  This allows you to compute.

2. Divide.  The following fraction works out evenly.  Many times this does not happen.  If that is the case be sure to read the directions on your assignment. Usually the directions will ask you to round to the nearest hundredth.  If there are no directions, it is safe to assume to round to the nearest hundredth.  This means you need to divide up to the thousandths place to determine whether you round up or not.

Bits & Pieces I Pretest

Bits & Pieces I Pretest